Blogs review: HP Filters and business cycles
What’s at stake: a recent speech by St. Louis Federal Reserve President James Bullard has launched a debate on the blogosphere over the use of a statistical technique called the Hodrick-Prescott filter. The technique – as well as so-called Bandpass filters – is used to decompose economic data into a trend and a cyclical component. The controversy came out as James Bullard pointed to these estimates – together with the fact that we don’t see deflationary pressures (see our review here) – as evidence that advanced economies are operating near potential, if not above.
Defining the trend and the cycle
Stephen Williamson writes that in studying the cyclical behavior of economic time series, one has to take a stand on how to separate the cyclical component of the time series from the trend component. One approach is to simply fit a linear trend to the time series. The problem with this is that there are typically medium-run changes in growth trends (e.g. real GDP grew at a relatively high rate in the 1960s, and at a relatively low rate from 2000-2012). If we are interested in variation in the time series only at business cycle frequencies, we should want to take out some of that medium-run variation. This requires that we somehow allow the growth trend to change over time. That's essentially what the HP filter does. The HP filter takes an economic time series y(t), and fits a trend g(t) to that raw time series, by solving a minimization problem. The trend g(t) is chosen to minimize the sum of squared deviations of y(t) from g(t), plus the sum of squared second differences, weighted by a smoothing parameter L (the greek letter lambda in the paper). The minimization problem penalizes changes in the growth trend, with the penalty increasing as L increases. The larger is L, the smoother will be the trend g(t).
Stephen Williamson notes that this approach was introduced to economists in the work of Kydland and Prescott, it became part of the toolbox used by people who worked in the real business cycle literature, and its use spread from there. Hodrick and Prescott's paper was unpublished for a long time, but appeared eventually in the Journal of Money, Credit, and Banking.
Noah Smith writes that if you are a "business cycle theorist", what you do for a living is basically this:
· Step 1: Subtract out a "trend"; what remains is the "cycle".
· Step 2: Make a theory to explain the "cycle" that you obtained in Step 1.
The Bullard controversy 2.0
Tim Duy points that St. Louis Federal Reserve President James Bullard (see the graph below taken from one of his recent speeches) likes to rely on this technique to support his claim that the US economy is operating near potential.
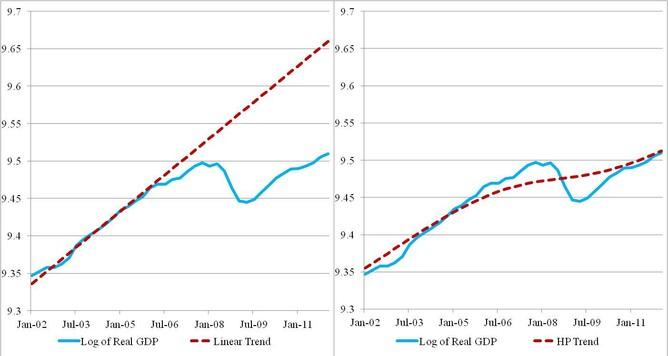
Click here to enlarge
Source: James Bullard (HT Tim Duy)
Paul Krugman writes that what is wrong with this view is that a statistical technique is only appropriate if the underlying assumptions behind that technique reflect economic reality — and that’s almost surely not the case here. The use of the HP filter presumes that deviations from potential output are relatively short-term, and tend to be corrected fairly quickly. In other words, the HP filter methodology basically assumes that prolonged slumps below potential GDP can’t happen. Instead, any protracted slump gets interpreted as a decline in potential output! For that reason, Brad DeLong writes that friends don’t let friends detrend data using the HP filter … that trick never works.
Tim Duy argues that these features are what makes the HP filter reveal a period of substantial above trend growth through the middle of 2008… contrary to what most people would believe.
The end point problem and CI for HP filters
Tim Duy points that if you don’t deal with the endpoint problem, you get that actual output is above than the HP trend – a proposition that most people would say is nonsensical. By itself, the issue of dealing with the endpoint problem should raise red flags about using the HP filter to draw policy conclusions about recent economic dynamics. Luís Morais Sarmento – economist at Banco de Portugal – explains that the end point problem results from the fact that the series smoothed by the HP-filter tend to be close to the observed data at the beginning and at the end of the estimation period. This problem is more important when the real output is far from the potential output. At Banco de Portugal, to address the end point problem, they expand the GDP series for some years, using their own projections of GDP growth, for the next years. Marianne Baxter and Robert King (1999) recommend dropping at least three data points from each end of the sample when using the Hodrick-Prescott filter on annual data.
David Giles (Econometrics Beat) has a new paper that develops a methodology for constructing confidence intervals for the HP filter. The application of the HP filter to extract the trend from a time-series amounts to signal extraction. Similarly, the estimation of a regression model extracts a signal about the dependent variable from the data, and separates it from the “noise”. In the case of a regression model it would be unthinkable to report estimated coefficients without their standard errors; or predictions without confidence bands. So, it is somewhat surprising that the trend that we extract from a time-series using the H-P filter is always reported without any indication of the uncertainty associated with it. The paper includes two applications: one application relates to the U.S. unemployment rate, and the other involves U.S. real value-added output.
Some important background papers on filtering
In their seminal paper, Charles Nelson and Charles Ploser (1982) investigates general characteristics of time-series of economics data for the US economy. The authors focus, in particular, on the question of whether the data is trend stationary (TS) – such that there is a deterministic (time-dependent) trend and a stochastic component – or if the data is difference-stationary (DS) – i.e. the underlying trends are stochastic. The difference matters both for constructing models – what kind of series models should produce – and for our general understanding of economic processes: if data are TS then current shocks in the variables do not matter for its long-run expected level; it data are DS, on the other hand, then all shocks are accumulated in the variable and their significance for the long-run level of the variable never decays.
Timothy Cogley and James Nason (1995) investigate the properties of the HP filter. The first problem (initially pointed by Charles Nelson and Heejoon Kang (1981) but reproduced in this paper) is that the HP filter can generate spurious cycles in DS processes. In other words, the "facts" about business cycles obtained from the HP-filtered data are often "artifacts". In essence what HP does is to decompose series into two parts – trend and deviation, where the trend includes all movements with a period of longer than 8 years (depending of course of the value of the lambda-parameter in the HP filter), while deviations contain all other movements. The problem is that after such decomposition this deviation component can demonstrate properties (e.g. in terms of auto- and cross-correlation functions, ACF and CCF) that could not be observed for the initial series. The nature of this problem is similar to that of Kuznets cycles: Simon Kuznets (1961) applied a filter to the data in an attempt to remove business cycles from it and observe longer, 20-year cycles. As it was shown later in Irma Adelman (1965) and Philip Howrey (1968) the properties of that filter were such, that is could generate 20-year cycles even in the white-noise series.
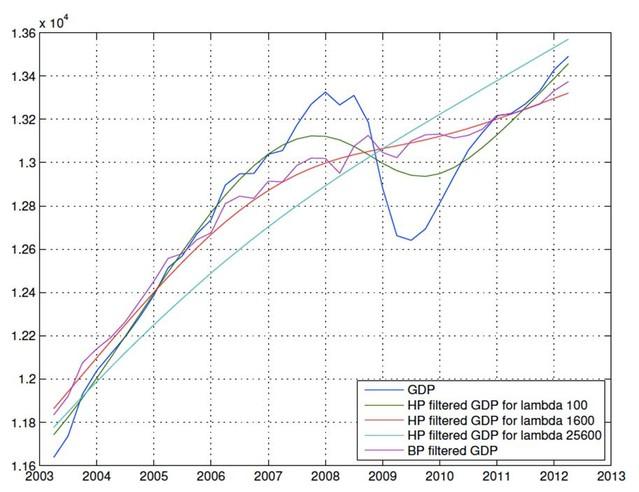
Click here to enlarge
Source: Own calculations. Note: the trend-cycle decompositions are based on the entire post-war period for the US economy. The graph only displays the results for the last decade.
Marianne Baxter and Robert King (1999) introduced a new filter (band-pass filter) for macro-data: they construct a filter that extracts the components from the data that have a periodicity between 6 and 32 quarters (periodicity that roughly meets the definition of business cycle). Despite the new method, the results produced by HP and band-pass filter are very similar (as can be seen in the figure that we produced above based on the latest real GDP data). So, it is not clear if the band-pass filter is not subject to same critique as HP filter. In a response to a reader comment, Stephen Williamson writes that a problem with the band-pass filters is that there is no such thing as a business cycle frequency. The Great Depression took a long time to work itself out, while some post-World War II recessions only lasted a few quarters.